- Элемент нумерованного списка
Структура данных «дерево»
Дерево целей:Структура данных «дерево»
- определения и общие понятия
- наглядный пример
- многие полезные структуры данных
- Двоичное дерево поиска
- АВЛ-дерево
- Красно-чёрное дерево
2.Структура продукта
2.1 Работа в Wiki 2.2 Презентация
3.Структура породукта
- Сбор информации (с 20 января по 1 февраля)
- 2.Сбор ссылок (с 1 по 7 февраля)
- 3.Размещение информации на сайте (с 7 по 17 февраля)
- 4.Структуирование информации (с 17 февраля по 1 марта)
- 5.Отформатирование информации (с 1 по 10 марта)
- 6.Создание презентации (с 10 по 18 марта)
- 7.Подготовка к выступлению (с 18 марта по 1 апреля)
Определение и общие понятие
- В информатике дерево - одна из наиболее широко распространённых структур данных, эмулирующая древовидную структуру в виде набора связанных узлов. Является связанным графом, не содержащим циклы. Большинство источников также добавляют условие на то, что рёбра графа не должны быть ориентированными. В дополнение к этим трём ограничениям, в некоторых источниках указываются, что рёбра графа не должны быть взвешенными.
Двои́чное де́рево http://dic.academic.ru/dic.nsf/ruwiki/147481— структура данных, являющаяся программной реализацией двоичного дерева (графа). Двоичное дерево состоит из узлов (вершин) — записей вида (data, left, right), где data — некоторые данные привязанные к узлу, left, right — ссылки на узлы, являющиеся детьми данного узла. Узел left называется левым ребёнком (сыном), а узел right — правым.
Существует следующее рекурсивное определение двоичного дерева (см. БНФ):
<дерево> ::= ( <данные> <дерево> <дерево> ) | nil .
То есть двоичное дерево либо является пустым, либо состоит из данных и двух поддеревьев (каждое из которых может быть пустым). Очевидным, но важным для понимания фактом является то, что каждое поддерево в свою очередь тоже является деревом. Если у некоторого узла оба поддерева пустые, то он называется листовым узлом (листовой вершиной).
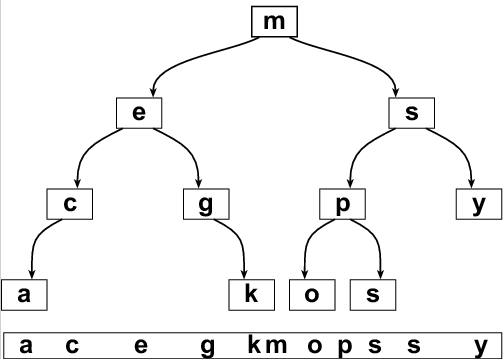
Пример
Все о двоичном дереве
Многие полезные структуры данных основаны на двоичном дереве:
Двоичное дерево поиска (binary search tree, BST) — это двоичное дерево, в котором данные, привязанные к каждому узлу, представляют собой пару (key, value) (ключ и значение), причём на ключах определена операция сравнения «меньше», и для всех узлов дерева выполнено свойство, называемое свойством дерева поиска:
у всех узлов левого поддерева произвольного узла n значение ключей меньше, нежели значения ключа узла n, у всех узлов правого поддерева произвольного узла n значение ключей не меньше, нежели значения ключа узла n.
Основные операции в двоичном дереве поиска
Базовый интерфейс двоичного дерева поиска состоит из трех операций:
FIND(K) — поиск узла, в котором хранится пара (key, value) с key = K. INSERT(K,V) — добавление в дерево пары (key, value) = (K, V). REMOVE(K) — удаление узла, в котором хранится пара (key, value) с key = K.
По сути, двоичное дерево поиска — это структура данных, способная хранить таблицу пар (key, value) и поддерживающая три операции: FIND, INSERT, REMOVE.
Кроме того, интерфейс двоичного дерева включает ещё три дополнительных операции обхода узлов дерева: INFIX_TRAVERSE, PREFIX_TRAVERSE и POSTFIX_TRAVERSE. Первая из них позволяет обойти узлы дерева в порядке неубывания ключей.
АВЛ-дерево
АВЛ-дерево — балансированное по высоте двоичное дерево поиска: для каждой его вершины высота её двух поддеревьев различается не более чем на 1.
АВЛ-деревья названы по первым буквам фамилий их изобретателей, Г. М. Адельсона-Вельского и Е. М. Ландиса, которые впервые предложили использовать АВЛ-деревья в 1962.
Алгоритм добавления вершины
Первый шаг аналогичен добавлению вершины в Двоичное дерево поиска. Далее производится балансировка всех предков добавленной вершины в порядке от родителя к корню. Относительно АВЛ-дерева балансировкой вершины называется операция, которая в случае разницы высот левого и правого поддеревьев = 2, изменяет связи предок-потомок в поддереве данной вершины так, что разница становится ⇐ 1, иначе ничего не меняет. Указанный результат получается вращениями поддерева данной вершины.
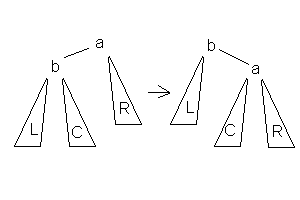
- 1.Малое правое вращение
 Данное вращение используется тогда, когда (высота b-поддерева - высота L) = 2 и высота С ⇐ высота R.
Данное вращение используется тогда, когда (высота b-поддерева - высота L) = 2 и высота С ⇐ высота R.
- 2.Большое правое вращение
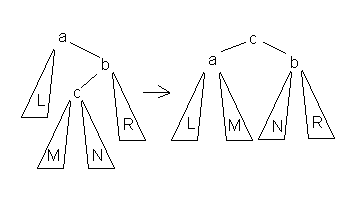 Данное вращение используется тогда, когда (высота b-поддерева - высота L) = 2 и высота c-поддерева > высота R.
Данное вращение используется тогда, когда (высота b-поддерева - высота L) = 2 и высота c-поддерева > высота R.
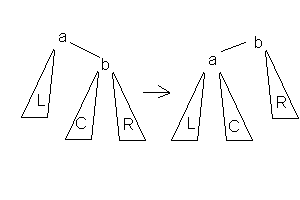
- Малое левое вращение
В каждом случае достаточно просто доказать то, что операция приводит к нужному результату и что полная высота уменьшается не более чем на 1 и не может увеличиться.
Из-за условия балансированности высота дерева О(lg(N)), где N- количество вершин, поэтому добавление элемента требует O(lg(N)) операций.
Красно-чёрное дерево
Красно-черное дерево (Red-Black-Tree, RB-Tree) — это одно из самобалансирующихся двоичных деревьев поиска, гарантирующих логарифмический рост высоты дерева от числа узлов и быстро выполняющее основные операции дерева поиска: добавление, удаление и поиск узла. Сбалансированность достигается за счет введения дополнительного атрибута узла дерева — «цвет». Этот атрибут может принимает одно из двух возможных значений — «чёрный» или «красный». Красно-чёрное дерево обладает следующими свойствами:
Корень и листья окрашены в чёрный цвет
Любой красный узел имеет только чёрных потомков
Все пути от корня к листьям имеют одинаковое число чёрных узлов
При этом для удобства листьями красно-чёрного дерева считаются фиктивные «нулевые» узлы, не содержащие данных. * пример: