При программировании на Delphi или Паскале иногда попадаются задачи, которые трудно «втиснуть» в стандартные конструкции языка. А решение лежит совсем рядом - в теории конечных автоматов. Мы не будем залезать в дебри, а просто покажем как это делается.

Давным-давно, когда люди еще не придумали объектно-ориентированное программирование, модным направлением было программирование структурное. Шутки шутками, но в результате именно структурного подхода мы сейчас имеем Pascal и Delphi.
Почему я говорю то Паскаль, то Дельфи? Просто потому, что лингвистическая основа Delphi - это Object Pascal, сильно выросший из детских штанишек, но все же узнаваемый. И новые объектно-ориентированные возможности и замечательные библиотеки классов в совокупности с CASE-средствами так и не скрыли полностью длинные уши структурного языка (и это замечательно!). Они вылезают то здесь, то там, в отдельных процедурах, в обработчиках событий…

Так вот, в те давние времена возникла следующая ситуация:

• «Сочинение» алгоритмов решения различных задач - процесс творческий, а творчество очень не любит каких-либо ограничений. Cтало быть алгоритм может быть любым, сколь угодно запутанным, образующим петли и прочие нелинейности.
• Стандартный Паскаль имеет очень ограниченное количество структурных инструкций ( if-then-else, while-do и т.д., вы это лучше меня знаете…)
• А программу-то написать хочется! Что делать ?
• А нельзя ли как-нибудь «втиснуть» этот наш премудрый алгоритм в куцый набор инструкций?
• Можно! Причем используя вполне формальное преобразование.
• Вот этим мы сейчас и займемся.

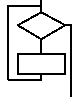
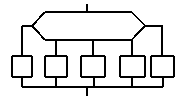
Итак, структурное программирование учит нас, что есть 5 основных конструкций, из которых как из кубиков строится любая процедура:

SEQUENCE	IF-THEN-ELSE	WHILE-DO	REPEAT-UNTIL	CASE

В нашем запутанном алгоритме наверняка не все так ужасно, как кажется. Скорее всего, там можно найти несколько фрагментов, подходящих под определение чисто структурных конструкций. Вопрос лишь в том, как эти конструкции соединить между собой.

А вот в этом как раз может помочь наша рабочая лошадка - непотопляемая конструкция REPEAT-CASE. При умелом применении эта нехитрая пара команд может «переварить» алгоритм любой сложности и запутанности. Главное, чтобы ВЫ четко представляли что делаете.

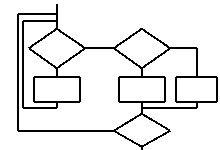
Предположим, у нас есть алгоритм следующего вида:

Хитрый ли он?
Да нет, конечно! Если приглядеться, он легко разбивается на 3 вложенные стандартные структуры:

Так что мы с легкой душой можем воплотить его в программе вроде такой:

repeat
  while C1 do B1;
  if C2 then B2
    else B3;
until C3;

Как было бы хорошо, если бы в жизни нам попадались только такие алгоритмы. Однако в таком случае, вам незачем было бы читать эту статью!

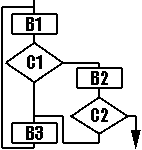Выглядит вроде просто, это мы мигом!
Гмм.. да.. пробуем и так и эдак - в стандартный Паскаль это явно не укладывается. Можно, конечно, попытаться «расшить» процедурные блоки B1 и B3 или применить GOTO или EXIT из цикла. Но все это, согласитесь, выглядит как-то жалко и самодеятельно. Опять же надо каждый раз думать где разомкнуть цикл…

И вот тут-то появляемся мы, (на белом коне ) с нашей универсальной отмычкой по имени REPEAT-CASE.

• Выделяем в нашем алгоритме фрагменты, которые хорошо укладываются в структурную модель (если такие есть). В нашем случае такой фрагмент только один: B2 + C2, т.е. последовательность из блока и условия.
• Вне этих фрагментов ставим жирные точки в следующих местах:
  • на входе в модуль (обозначим ее 1)
  • на выходе модуля (обозначим 0)
  • на входах и выходах всех фрагментов, что мы нашли
  • во всех местах, где есть пересечение линий на блок-схеме

• Пронумеруем оставшиеся точки произвольно. Позже мы еще поговорим о том, что могут на самом деле означать эти номера. В нашем примере получается 4 точки от 0 до 3.
• Теперь мы готовы перейти к модели конечного автомата и написать-таки нашу программу.
• Представьте, что есть некий блок, который может находиться в одном из 4 состояний. И есть набор действий, в результате которых блок переходит из одного состояния в другое.
• Для отображения этого самого состояния, заведем в программе некоторую переменную, скажем, State. А внутри веток CASE будем изменять ее состояние.

• Пишем нашу программу:

var State:integer;
begin
  State:=1;  {для любого алгоритма}
  repeat
    case State of
...
    end;
  until State=0; {тоже для любого алгоритма}
end;

• Теперь пропишем ветки CASE. Не забудьте в конце каждой ветки уточнить состояние:

    case State of
1: begin B1; if C1 then State:=2 else State:=3 end;
2: begin B2; if C2 then State:=0 else State:=3 end;
3: begin B3; State:=1 end;
    end;

• Все! Программа готова. Идите и попробуйте, она работает. И с точки зрения логики Паскаля все безупречно - никаких тебе GOTO и прочих неприятностей.

А теперь, после того, как мы добились столь блестящего результата, давайте осознаем: что же мы сделали и что у нас получилось.

• Мы изобразили наш алгоритм как блок-схему или, другими словами, направленный граф
• Затем провели инвариантное преобразование этого графа с выделением нескольких стационарных состояний программы - конечного автомата
• В результате получили новый граф, который легко укладывается в структурные конструкции Паскаля (Delphi)

Проводя указанные действия несколько раз для разных алгоритмов, можно заметить, что на самом деле наши произвольно расставленные точки-состояния не такие уж случайные и произвольные. Как правило, при более глубоком рассмотрении вашего конкретного алгоритма можно найти каждому из этих состояний свое название. Это название может быть гораздо более выразительным, чем просто 1-2-3, поскольку это действительно состояния вашей программы.

О чем я говорю? Пусть ваш алгоритм занимается, скажем, синтаксическим разбором HTML-файла. Тогда одно из состояний может звучать как «Обнаружен тэг BODY» или «Найден конец документа».

Паскаль предлагает нам замечательное средство для работы с такими обозначениями в символическом виде и об этом средстве сейчас часто забывают. Программа из нашего примера может выглядеть так:

var State:(START, EOF_found, Line_Added, DONE);
begin
  State:=START;  {для любого алгоритма}
  repeat
    case State of
START:      begin B1; if C1 then State:=EOF_Found else State:=Line_Added end;
EOF_Found:  begin B2; if C2 then State:=DONE else State:=Line_Added end;
Line_Added: begin B3; State:=START end;
    end;
  until State=DONE; {тоже для любого алгоритма}
end;

Замечательно, что Delphi все еще поддерживает эту спецификацию и даже показывает при отладке символьное представление состояния! Это очень удобно на практике. Спасибо, Borland!

Возможно вы, как и я, проделав подряд несколько таких преобразований и войдя во вкус, заметите, что стали мыслить при программировании чуть-чуть иначе. Иногда, особенно когда задача несколько запутана, хочется сразу выделить несколько важных состояний и строить обработчик уже вокруг них. Это правильное желание, ему стоит потакать.

Кстати, сейчас тема конечных автоматов вновь стала актуальной и то и дело мелькает на страницах компьютерных журналов.

• http://pascal.sources.ru/articles/formal.htm#FORMAL
• www.citforum.ru/programming/digest/formal.shtml
• http://ru.wikipedia.org/wiki/Конечные_автоматы

• http://ru.wikipedia.org/wiki/Теория_графов
• http://algolist.manual.ru/