Алгоритмы бинарного поиска
Двоичный (бинарный) поиск (также известен как метод деления пополам и дихотомия) — классический алгоритм поиска элемента в отсортированном массиве (векторе). Также применяется для нахождения заданного значения монотонной (невозрастающей или неубывающей) функции. Поиск основывается на теореме о промежуточных значениях. Используется в информатике, вычислительной математике и математическом программировании.
В ряде случаев (в частности, в задачах интерполяции) приходится выяснять, где по отношению к заданному упорядоченному массиву действительных чисел располагается заданное действительное число. В отличие от поиска в массиве целых чисел, заданное число в этом случае чаще всего не совпадает ни с одним из чисел массива, и требуется найти номера элементов, между которыми это число заключено.
Один из наиболее быстрых способов этого является бинарный поиск, характерное число операций которого имеет порядок log2(n), где n – число элементов массива. При многочисленных обращениях к этой процедуре число операций будет равно m log2(n) (m – число обращений). Ускорения этой процедуры можно добиться за счет сохранения предыдущего результата операции и попыток поиска при новом обращении в ближайших узлах массива с дальнейшим расширением области поиска в случае неуспеха.
При этом в наихудших случаях число операций будет больше (примерно в 2 раза) по сравнению с бинарным поиском, но обычно при m значительно большим, чем log2(n) удается довести порядок числа операций до m, то есть сделать его почти независимым от размера массива.
Важным примером применения подобного алгоритма является картирование области: по заданному массиву RGB-палитры, соответствующему 'уровням' карты, раскрасить эту область, определив цвет каждого пиксела. Значение, соответствующее пикселу, считается заданным (найденным каким-либо внешним по отношению к программе раскрашивания способом); по нему определяется, между какими уровнями карты оно находится, а по этим номерам определяется его цвет, получаемый из палитры.
Число уровней при этом может быть достаточно большим, изменение же уровня между соседними пикселами – чаще всего слабым. В этом случае ускорение, порождаемое алгоритмом по сравнению со стандартным бинарным поиском, является весьма существенным.
Задача ставится так. Дан упорядоченный массив действительных чисел array размерности n, проверяемое значение value и начальное приближение узла old. Требуется найти номер узла res массива array, такой, что array[res]⇐value<array[res+1]
Алгоритм работает следующим образом.
1. Определяется, лежит ли проверяемое value за пределами массива array. В случае value<array[0] возвращается -1, в случае value>array[n-1] возвращается n-1.
2. Иначе проверяется: если значение old лежит за пределами индексов массива (т.е. old<0 или old>=n, то переходим к обычному бинарному поиску, установив левую границу left=0, правую right=n-1.
3. Иначе переходим к выяснению границ поиска. Устанавливается left=right=old, inc=1 – инкремент поиска.
4. Проверяется неравенство value>=array[old]. При его выполнении переходим к следующему пункту (5), иначе к пункту (7).
5. Правая граница поиска отводится дальше: right=right+inc. Если right>=n-1, то устанавливается right=n-1 и переходим к бинарному поиску.
6. Проверяется value>=array[right]. Если это неравенство выполняется, то левая граница перемещается на место правой: left=right, inc умножается на 2, и переходим назад на (5). Иначе переходим к бинарному поиску.
7. Левая граница отводится: left=left-inc. Если left⇐0, то устанавливаем left=0 и переходим к бинарному поиску.
8. Проверяется value<array[left]. При выполнении правая граница перемещается на место левой: right=left, inc умножается на 2, переходим к пункту (7). Иначе к бинарному поиску.
9. Проводится бинарный поиск в массиве с ограничением индексов left и right. При этом каждый раз интервал сокращается примерно в 2 раза (в зачисимости от четности разности), пока разность между left и right не достигнет 1. После этого возвращаем left как результат, одновременно присваивая old=left.
Ниже приведена программа на C, реализующая алгоритм поиска в упорядоченном массиве действительных чисел.
/* Search within a real ordered array.
Parameters:
value -- the sample,
old -- previous result,
array,n -- the array and its dimension.
Returns: Left node of the array segment matching the sample.
In case the sample is out of the array, returns -1 (less than
left boundary) or (n-1) (more than the right boundary).
*/ int fbin_search(float value,int *old,float *array,int n) {
register int left,right;
/* проверка позиции за пределами массива */
if(value < array[0]) return(-1);
if(value >= array[n-1]) return(n-1);
/* процесс расширения области поиска. Вначале проверяется валидность
начального приближения */
if(*old>=0 && *old<n-1) {
register int inc=1;
left = right = *old;
if(value < array[*old]) {
/* область расширять влево */
while(1) {
left -= inc;
if(left <= 0) {left=0;break;}
if(array[left] <= value) break;
right=left; inc<<=1;
}
}
else {
/* область расширять вправо */
while(1) {
right += inc;
if(right >= n-1) {right=n-1;break;}
if(array[right] > value) break;
left=right; inc<<=1;
}
}
}
/* начальное приближение плохое - :-P
за область поиска принимается весь массив */
else {left=0;right=n-1;}
/* ниже алгоритм бинарного поиска требуемого интервала */
while(left<right-1) {
register int node=(left+right)>>1;
if(value>=array[node]) left=node;
else right=node;
}
/* возвращаем найденную левую границу,
обновив старое значение результата */
return(*old=left);
}
Замечание: для успешной работы алгоритма целесообразно при первичном запуске положить *old=-1 или другое число, гарантирующее бинарный поиск на первом проходе.
Бинарный поиск в массиве
На практике довольно часто производится поиск в массиве, элементы которого упорядочены по некоторому критерию (такие массивы называются упорядоченными). Например, массив фамилий, как правило, упорядочен по алфавиту, массив данных о погоде — по датам наблюдений. В случае, если массив упорядочен, то применяют другие, более эффективные по сравнению с методом простого перебора алгоритмы, один из которых — метод бинарного поиска. Пусть есть упорядоченный по возрастанию массив целых чисел. Нужно определить, содержит ли этот массив некоторое число (образец). Метод (алгоритм) бинарного поиска реализуется следующим образом:
1. Сначала образец сравнивается со средним (по номеру) элементом массива Если образец равен среднему элементу, то задача решена. Если образец больше среднего элемента, то это значит, что искомый элемент расположен ниже среднего элемента (между элементами с номерами sred+1 и niz), и за новое значение verb принимается sred+i, а значение niz не меняется Если образец меньше среднего элемента, то это значит, что искомый элемент расположен выше среднего элемента (между элементами с номерами verh и sred-1), и за новое значение niz принимается sred-1, а значение verh не меняется
2. После того как определена часть массива, в которой может находиться искомый элемент, по формуле (niz-verh) /2+verh вычисляется новое значение sred и поиск продолжается.
unit b_found_;
interface
uses
Windows, Messages, SysUtils, Classes,
Graphics, Controls, Forms, Dialogs, StdCtrls, Grids;
type
TForm1 = class(TForm)
Label1: TLabel;
Label2: TLabel;
Button1: TButton;
Label3: TLabel;
CheckBox1: TCheckBox;
StringGrid1: TStringGrid;
Editl: TEdit;
procedure ButtonlClick(Sender: TObject);
procedure StringGridlKeyPress(Sender: TObject; var Key: Char);
procedure EditlKeyPress(Sender: TObject; var Key: Char);
private
{Private declarations }
public
{ Public declarations }
end;
var
Form1: TForm1;
implementation
{$R *.DFM}
{ Бинарным поиск в массиве }
procedure TForm1.Button1Click(Sender: TObject);
const
SIZE = 10;
var
a: array[1..SIZE] of integer; { массив }
obr: integer; { образец для поиска}
verh: integer; { верхняя граница поиска }
niz: integer; { нижняя граница поиска }
sred: integer; { номер среднего элемента }
found: boolean; { TRUE — совпадение образца с элементом массива }
n: integer; { число сравнений с образцом}
i: integer;
begin
// ввод массива и образца
for i := l to SIZE do
a[i] := StrToInt(StringGridl.Cells[i - l, 0]);
obr := StrToInt(Editl.text);
// поиск verh:=1;
niz := SIZE; n := 0;
found := FALSE; labels.caption := '';
if CheckBoxl.State = cbChecked then
Labels.caption: = 'verh' + #9 + 'niz'#9'sred' #13;
// бинарный поиск в массиве
repeat
sred := Trunc((niz - verh) / 2) + verh;
if CheckBox1.Checked then
Labels.caption := label3.caption + IntToStr(yerh) + #9
+ IntToStr(niz) + #9 + IntToStr(sred) + #13; n := n + 1;
if a[sred] = obr then
found := TRUE
else
if obr < a[sred] then
niz := sred - 1
else
verh := sred + 1;
until
(verh > niz) or found;
if found then
labels.caption := label3.caption
+ 'Совпадение с элементом номер '
+ IntToStr(sred) + #13 + 'Сравнений '
+ IntToStr(n)
else
label3.caption := label3.caption
+ 'Образец в массиве не найден.';
end;
// нажатие клавиши в ячейке StringGrid
procedure TForml.StringGridlKeyPress(Sender: TObject; var Key: Char),
begin
if Key = #13 then // нажата клавиша <Enter>
// курсор в следующую ячейку таблицы
if StringGrid1.Col < StringGridl.ColCount - 1 then
StringGridl.Col := StringGrid1.Col + 1
else // курсор в поле Editl, в поле ввода образца
Editl.SetFocus;
end;
// нажатие клавиши в поле Editl
procedure TForm1.Edit1KeyPress(Sender: TObject; .var Key: Char);
begin
// нажата клавиша <Enter>
if Key = #13 then // сделать активной командную кнопку
Button1.SetFocus;
end;
end.
DelphiWorld 6.0
function FoundByBinarySearch(
LowIdx,
HighIdx: LongInt;
var Result: LongInt;
const GoalIs: CompareFunc;
var Data;
var Goal
): Boolean;
var
CompVal: CompareResults;
begin
FoundByBinarySearch := FALSE;
if HighIdx < LowIdx then
Exit;
Result := LowIdx + ((HighIdx - LowIdx) div 2);
CompVal := GoalIs(Result, Data, Goal);
if CompVal = BinEqual then
FoundByBinarySearch := TRUE
else if (LowIdx < HighIdx) then
begin
if CompVal = BinLess then
HighIdx := Result - 1
else {CompVal = BinGreater}
LowIdx := Result + 1;
FoundByBinarySearch := FoundByBinarySearch(
LowIdx, HighIdx, Result, GoalIs, Data, Goal)
end
else if (CompVal = BinLess) then
Dec(Result)
end; { function FoundByBinarySearch }
DelphiWorld 6.0
Написание программы, которая осуществляет бинарный поиск элемента в отсортированном массиве
Разработка алгоритма
Бинарный поиск необходимо производить в предварительно отсортированном массиве. Находится средний элемент массива и сравнивается с искомым значением. Если они равны, то поиск завершен, если искомое значение меньше значения среднего элемента, то дальнейший поиск производится в левой половине массива, иначе – в правой. Алгоритм поиска:
1. Определить средний элемент массива
2. Если его значение равно искомому, значит элемент найден. Перейдем к шагу 6
3. Если количество элементов массива равно 1, значит элемент не найден. Перейдем к шагу 6
4. Если искомое значение меньше значения среднего элемента, то возьмем в качестве массива все элементы слева от среднего и перейдем к шагу 1
5. возьмем в качестве массива все элементы справа от среднего и перейдем к шагу 1
6. Конец
Описание метода решения
Поиск нужного значения среди элементов отсортированного массива начинается с определения значения центрального элемента этого массива. Оно сравнивается с искомым значением и в зависимости от результатов сравнения предпринимаются определенные действия. Если искомое и центральное значения оказываются равны, то поиск завершается успешно. Если искомое значение меньше центрального или больше, то формируется массив, состоящий из элементов, находящихся слева или справа от центрального соответственно. Затем поиск повторяется в новом массиве. В программе алгоритм реализован с применением рекурсии.
Создание первоначального массива происходит путем загрузки его элементов из текстового файла. Числа в файле должны быть записаны через пробел.
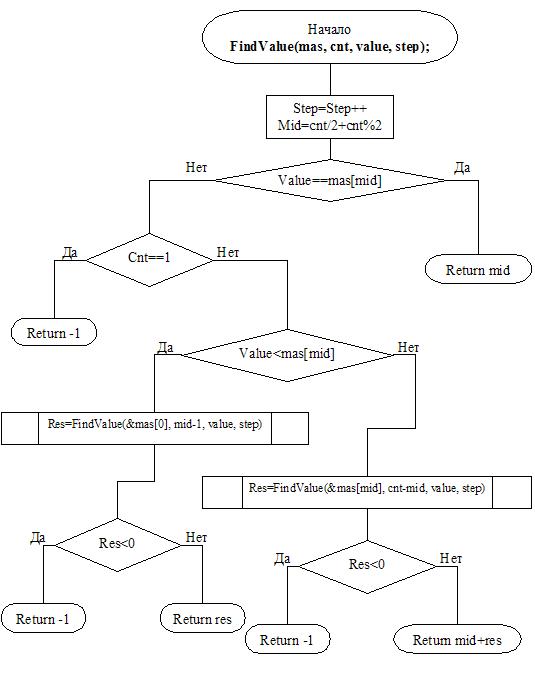
Блок - схема алгоритма
Пример работы программы
< < < Б и н а р н ы й п о и с к > > >
Введите имя файла с массивом чисел: test.txt
Загрузка массива:
23 45 10 -4 8 1 0 8 39
Загружено 9 элементов массива.
Загружен следующий массив A[9]:
[ 23 45 10 -4 8 1 0 8 39 ]
Проведем сортировку массива:
Итоговый массив:
[ -4 0 1 8 8 10 23 39 45 ]
Найти элемент массива v=10
Начинаем бинарный поиск.
Итерация № 1, массив для поиска: [ -4 0 1 8 8 10 23 39 45 ]
10>8
Итерация № 2, массив для поиска: [ 10 23 39 45 ]
10<23
Итерация № 3, массив для поиска: [ 10 ]
10==10
Элемент 10 найден в 6-й позиции на 3-й итерации.
Искать другой элемент? (ENTER - да)
Исходный текст программы
Программа написана на языке программирования Borland C++.
Ниже приведен листинг файла bin_srch.cpp.
//Бинарный поиск
#include <bios.h>
#include <stdio.h>
#include <conio.h>
#include <stdlib.h>
#include <fstream.h>
#include <io.h>
void GetArray(int *mas, int &cnt) //функция загрузки массива из файл
{
cnt=0;
int v;
char *fn="";
cout<<"Введите имя файла с массивом чисел: ";
cin>>fn;
if (access(fn, 0)!=0) //проверим наличие файла
{
cout<<"\nОшибка: Не удается открыть файл!!!\n";
bioskey(0);
exit(1);
}
cout<<"\nЗагрузка массива:\n";
ifstream fin(fn);
while (!fin.eof()) //загрузим все элементы из файла и определим их количество
{
fin>>v;
if (!fin.eof())
{
cnt++;
mas[cnt]=v;
cout<<" "<<v;
}
}
cout<<"\nЗагружено "<<cnt<<" элементов массива.\n";
fin.close();
}
void ShowArray(int *mas, int cnt) //функция вывода массива на экран
{
cout<<"[";
for (int i=1; i<=cnt; i++) {printf("%3d ", mas[i]);}
cout<<"]\n";
}
void SortArray(int *mas, int cnt) //функция сортировки массива (методом выбора)
{
int tmp;
int min=1;
for (int i=1; i<cnt; i++)
{
min=i;
for (int j=i; j<=cnt; j++)
{
if (mas[j]<mas[min]) {min=j;}
}
tmp=mas[min];
mas[min]=mas[i];
mas[i]=tmp;
}
}
int FindValue(int *mas, int cnt, int value, int &step) //рекурсивная функция для поиска элемента в массиве
{
step++;
cout<<"Итерация № "<<step<<", массив для поиска: ";
ShowArray(mas, cnt);
int res;
int mid=(cnt/2)+(cnt%2); //определим середину массива
if (value==mas[mid]) //если элемент оказался в середине, то нашли!
{
cout<<" "<<value<<"=="<<mas[mid]<<"\n\n";
return mid;
}
if (cnt<=1) {return -1;}
if (value<mas[mid]) //если значение меньше среднего элемента массива, то ищем в левой части
{
cout<<" "<<value<<"<"<<mas[mid]<<"\n\n";
res=FindValue(&mas[0], (mid-1), value, step);
if (res<0) {return -1;}
return res;
}
else //если же значение больше среднего элемента массива, то ищем в правой части
{
cout<<" "<<value<<">"<<mas[mid]<<"\n\n";
res=FindValue(&mas[mid], (cnt-mid), value, step);
if (res<0) {return -1;}
return mid+res;
}
}
void main()
{
int N; //количество элементов в массиве
int A[256]; //массив
clrscr();
cout<<"\n < < < Б и н а р н ы й п о и с к > > >\n\n";
GetArray(A, N); //загрузи массив
printf("\nЗагружен следующий массив A[%d]:\n", N);
ShowArray(A, N);
printf("\nПроведем сортировку массива:\n");
SortArray(A, N); //отсортируем массив для поиска
int v; //искомое значение
int i; //позиция найденного элемента в массиве
char ch;
do {
int j=0; //количество итераций
printf("Итоговый массив:\n");
ShowArray(A, N);
printf("\nНайти элемент массива v=");
cin>>v;
printf("\nНачинаем бинарный поиск.\n");
i=FindValue(A, N, v, j);
if (i<=0) {printf("\nЭлемент %d в массиве не найден!\n", v);}
else {printf("\nЭлемент %d найден в %d-й позиции на %d-й итерации.\n", v, i, j);}
printf("\nИскать другой элемент? (ENTER - да)\n\n");
ch=bioskey(0);
clrscr();
} while (ch==13);
}
Применение
Практическое применение метода двоичного поиска очень широко. Перечислим основные способы:
Самое широкое распространение метод получил в информатике для навигации (поиска) в структурах данных. Также его применяют в качестве численного метода для нахождения приближённого решения уравнений. Метод служит для нахождения экстремума целевой функции и в этом случае является методом условной одномерной оптимизации. Когда функция имеет вещественный аргумент, найти решение с точностью до можно за время , где . Когда аргумент дискретен, и изначально лежит на отрезке длины N, поиск решения займёт времени.
Применительно к массивам данных, поиск осуществляется по ключу, присвоенному каждому из элементов массива (в простейшем случае сам элемент является ключом).
Двоичный поиск как численный метод решения уравнений предполагает поиск нуля, о чём уже было сказано в описании.
Наконец, для поиска экстремума, скажем для определённости минимума, на очередном шаге отбрасывается тот из концов рассматриваемого отрезка, значение в котором максимально.