Системы счисления
Цели: познакомить учащихся с историей возникновения и развития систем счисления; указать на основные недостатки и преимущества непозиционных систем счисления.
Требования к знаниям и умениям:
Учащиеся должны знать:
• Определение следующих понятий: «цифра», «число», «система счисления», «непозиционная система счисления»;
• Недостатки непозиционных систем счисления.
Учащиеся должны уметь:
• Записывать числа в непозиционных системах счисления.
Программно-дидактическое обеспечение: ПК, слайды.
Ход урока
I. Постановка целей урока
1). «Все есть число». Что имели в виду древние пифагорейцы?
2). Сколько существует систем развития? Какая была самой первой и почему?
3). Римское число СХХVII .Какую величину оно выражает?
II. Изложение нового материала
1. Системы счисления
Лозунг «Все есть число». Так говорили пифагорейцы, подчеркивая необычайно важную роль чисел в практической деятельности. Современный человек каждый день запоминает номера машин и телефонов, в магазине подсчитывает стоимость покупки, ведет семейный бюджет и т.д. и т.п. Числа, цифры … они с нами везде.
Люди всегда считали и записывали числа, даже пять тысяч лет назад. Но записывали они их совершенно по-другому, по другим правилам. Но в любом случае число изображалось с помощью любого или нескольких символов, которые называются цифрами.
Цифры – это символы, участвующие в записи числа и составляющие некоторый алфавит.
Что же тогда число?
Первоначально число было привязано к тем предметам, которые пересчитывались. Но с появлением письменности число отделилось от предметов пересчета и появилось понятие натурального числа. Дробные числа появились в связи с тем, что человеку потребовалось что-то измерять и единица измерения (эталон) не всегда укладывалась целое число раз в измеряемой величине. Далее понятие числа развивалось в математике и сегодня считается фундаментальным понятием не только математики, но и информатики.
Число – это некоторая величина.
Числа складываются из цифр по особым правилам. На разных этапах развития человечества, у разных народов эти правила были различны и сегодня мы их называем системами счисления.
Система счисления – это способ записи чисел с помощью цифр.
Все известные системы счисления делятся на позиционные и непозиционные. Непозиционные системы счисления возникли раньше позиционных. Последние являются в свою очередь результатом длительного исторического развития непозиционных систем счисления.
Непозиционной называется такая система счисления, у которой количественный эквивалент («вес») цифры не зависит от ее местоположения в записи числа.
Например, рассмотрим римское число VVV. В десятичной системе счисления это число 15. При записи числа VVV использовались одинаковые «цифры» -V. И если сравнить их между собой, то получим абсолютное равенство. Т.е. на каком бы месте ни стояла цифра в записи числа, ее «вес» всегда один и тот же. В данном примере он равен 5.
2. Непозиционные системы счисления
1. Единичная система счисления.
В древние времена, когда люди начали считать, появилась потребность в записи чисел. Количество предметов, например, мешков, изображалось нанесением черточек или засечек на какой-либо твердой поверхности: камне, глине, дереве (до изобретения бумаги было еще очень далеко). Каждому мешку в такой записи соответствовала одна черточка. Археологами найдены такие «записи» при раскопках культурных слоев, относящихся к периоду палеолита (10 – 11 тысяч лет до н.э.).
Ученые назвали этот способ записи чисел единичной или унарной системой счисления. Неудобства такой системы очевидны: чем большее число надо записать, тем больше палочек. При записи большого числа легко ошибиться – нанести лишнее количество палочек или, наоборот, не дописать палочки.
Поэтому позже эти значки стали объединять в группы по 3,5 и 10 палочек. Таким образом, возникали уже более удобные системы счисления. Отголоски единичной системы счисления встречаются и сегодня. Например, сами того не осознавая, малыши на пальцах показывают свой возраст, а счетные палочки использовали для обучения счету учеников первого класса.
2. Древнеегипетская десятичная непозиционная система счисления.
Древнеегипетская десятичная непозиционная система возникла во второй половине третьего тысячелетия до н. э. бумагу заменяла глиняная дощечка, и именно поэтому цифры имеют такое написание. В этой системе счисления использовали в качестве цифр ключевые числа 1, 10, 100, 1000 и т. д. и записывались в виде иероглифов.
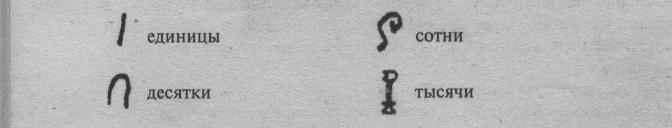
Именно из комбинаций таких «цифр» записывались числа и каждая «цифра» повторялась не более 9 раз.
- Почему? (Так как 10 подряд идущих одинаковых цифр можно заменить одним числом, но на разряд старше. Например )
Все остальные числа составлялись из этих ключевых при помощи обычного сложения. Вначале писали число высшего порядка, а за тем низшего.
Пример 1
Число 2376 «рисовалось» так:
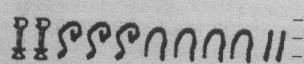
1. два цветка лотоса (две тысячи);\\ 2. три свернутых пальмовых листа (три сотни);\\ 3. четыре дуги (четыре десятка);\\ 4. два шеста (две единицы).\\
Умножение и деление египтяне производили путем последовательного удвоения чисел – особая роль отводилась двойке.
Пример 2
Египтяне вычисляли 19*31 так: они последовательно удваивали число 31. В правом столбце записывали результаты удвоения, а в левой – соответствующую степень двойки.
| 1 | 31 |
| 2 | 62 |
| 4 | 124 |
| 8 | 248 |
| 16 | 496 |
Затем отмечали вертикальными черточками строки левого столбца, из которых можно было сложить множитель (19=1+2+16), и складывали числа, стоящие в отмеченных строках справа (31+62+496=589).
3. Римская система счисления
Знакомая нам римская система принципиально не намного отличается от египетской. Но она более распространена в наши дни: в книгах, фильмах.
В ней для обозначения чисел используются знаки I (один палец) для числа один, V (раскрытая ладонь) для числа пять, Х (две сложенные ладони) для числа десять, а для чисел 50, 100, 500 и 1000 используются заглавные латинские буквы соответствующих латинских слов (Сеntum – сто, Demimille – половина тысячи, Мille – тысяча)V,X,L,C,D и М (соответственно); являющиеся « цифрами» этой системы счисления. Число в римской системе счисления обозначается набором стоящих подряд «цифр».
В римской системе счисления для обозначения цифр использовались следующие латинские буквы:
I – 1, V – 5, X – 10, L – 50, C – 100, D – 500, M – 1000.
Правила составления чисел в римской системе счисления:
Число равно:
1) сумме значений идущих подряд нескольких одинаковых «цифр» (назовем их группой первого вида);
2) разности значений двух «цифр», если слева от большей «цифры» стоит меньшая. В этом случае от значения большей «цифры» отнимается значение меньшей «цифры». Вместе они образуют группу второго вида. Заметим, что левая «цифра» может быть меньше правой максимум на один порядок: так перед L(50) и С(100) из «младших» может стоять только Х(10), перед V(5) - только I(1);
3)сумме значений групп и «цифр», не вошедших в группы первого или второго вида.
Пример 3
Записать число 444 в римской системе счисления.
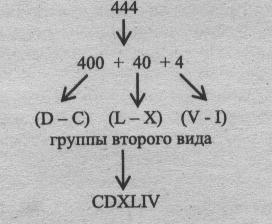
Пояснение: обратите внимание учеников на то, что в десятичной записи числа используются 3 одинаковые цифры, а в римской системе счисления – разные.
Пример 4
Записать число 1986 в римской системе счисления.
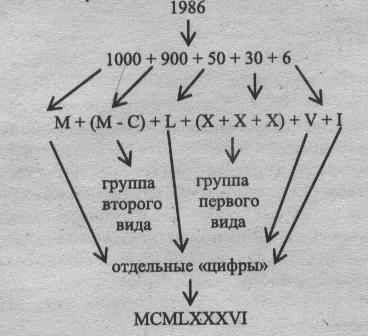
4. Как считали греки
Греки применяли несколько способ записи чисел. Афиняне для обозначения чисел пользовались первыми буквами слов-числительных:
Г (Гɛντɛ) – пять,
∆ (∆ɛκα) – десять,
Н (Нκατоν) – сто,
Х (Хιλιασ) – тысяча,
М (Мυριασ) – десять тысяч,
I, II, III, IIII – 1, 2, 3, 4,
∆∆∆IIII – 10+10+10+4=34.
С помощью этих цифр житель Древней Греции мог записать любое число.
Великий греческий математик Диофант Александрийский записывал дроби примерно так, как принято сейчас: числитель над знаменателем, но без черты. Это был один из способов записи дробей в Древней Греции.
5. Алфавитные системы
Более совершенными непозиционными системами счисления были алфавитные системы. К числу таких систем счисления относились славянская, ионийская (греческая), финикийская и другие. В них числа от 1 до 9, целые количества десятков (от 10 до 90) и целые количества сотен (от 100 до 900) обозначались буквами алфавита.
Алфавитная система была принята и в древней Руси. До конца 17 века (до реформы Петра I) в ней в качестве «цифр» использовались 27 букв кириллицы.
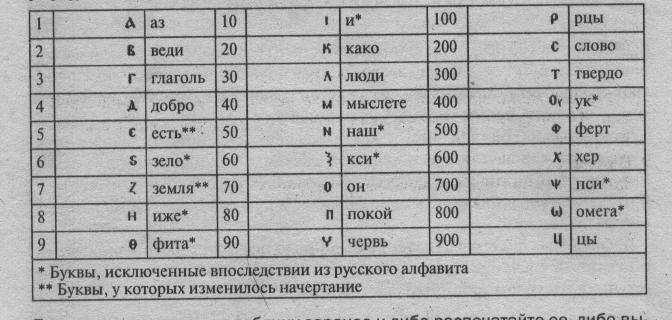
Пояснение: подготовьте таблицу заранее и либо распечатайте ее, либо выполните ее в виде плаката.
Чтобы отличать буквы от цифр над буквами ставился специальный знак ҃ титло. Это делалось для того, чтобы отличить числа от обычных слов:
Интересно, что числа от 11 (один – на десять) до 19 (девять – на десять) записывали так же, как говорили, то есть «цифру» единиц ставили до «цифры» десятков. Если число не содержало десятков, то «цифру» десятков не писали.
Удобны ли алфавитные системы?
Пример 5 (все вместе). Запишем числа 23 и 444 в славянской системе счисления.

Мы видим, что запись получилась не длиннее нашей десятичной. Это объясняется тем, что в алфавитных системах использовалось, по крайней мере, 27 «цифр». Но эти системы были удобны только для записи чисел до 1000.
Правда, славяне, как и греки, умели записывать числа и больше 1000. Для этого к алфавитной системе добавляли новые обозначения. Так, например, числа 1000, 2000, 3000… записывали теми же «цифрами», что и 1, 2, 3…, только перед «цифрой» ставили слева снизу специальный знак .
Число 10000 обозначалось той же буквой, что и 1, только без титла, ее обводили кружком. Называлось это число «тьмой». Отсюда и произошло выражение «тьма народу».

Таким образом, для обозначения «тем» (множественное число от слова тьма) первые 9 «цифр» обводились кружками.
10 тем, или 100 000, было единицей высшего разряда. Ее называли «легион». 10 легионов составляли «леорд». Самая большая из величин, имеющих свое обозначение, называлась «колода», она равнялась 1050. Считалось, что «боле сего несть человеческому уму разумевати».
Такой способ записи чисел, как в алфавитной системе, можно рассматривать как зачатки позиционной системы, так как в нем для обозначения единиц разных разрядов применялись одни и те же символы, к которым лишь добавлялись специальные знаки для определения значения разряда.
Алфавитные системы счисления были мало пригодны для оперирования с большими числами. В ходе развития человеческого общества эти системы уступили место позиционным системам.
III. Закрепление изученного
Решите задачи:
№1
Какие числа записаны с помощью римских цифр: ММIV, LХV, СМLХIIV?
№2
Запишите число 555:
А) в древнеегипетской системе счисления;
Б) в римской системе счисления;
В)в древнеславянской системе счисления.
№3
Запишите числа от 15 до 25 в старославянской системе счисления.
№4
Выполните действия:
А) МММD + LХ
Б)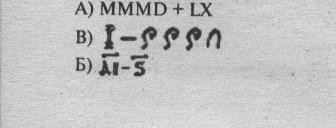
В)
IV. Итоги урока
Оцените работу класса и назовите учащихся, отличившихся на уроке.
Домашнее задание
Уровень знания: по материалу урока заполните таблицу:
| Название системы счисления | Цифры данной системы счисления | Десятичное число | Запись числа в данной системе счисления |
|---|---|---|---|
| 12 | |||
| 17 | |||
| 21 | |||
| 33 |
Уровень понимания: запишите с помощью известных вам непозиционных систем счисления дату своего рождения.
Уровень применения:
1. Некоторые римские цифры легко изобразить с помощью палочек.
Исправьте неверные равенства, переложив с одного места на другое только одну палочку.
VII – V = ХI IХ – V = VI
VI – I = III VIII – III = Х
2. Придумайте свою непозиционную систему счисления, указав при этом:
-какие знаки используются в качестве цифр;
-правила, по которым формируются из этих цифр числа.
Запишите в ней числа 352, 2004, 25.
Задание выполните на отдельных карточках.
Творческий уровень: напишите свою биографию, используя римскую систему счисления. Используйте для этого свой домашний компьютер.