Оценка сложности алгоритмов: интуитивный и научный подход
Логотип
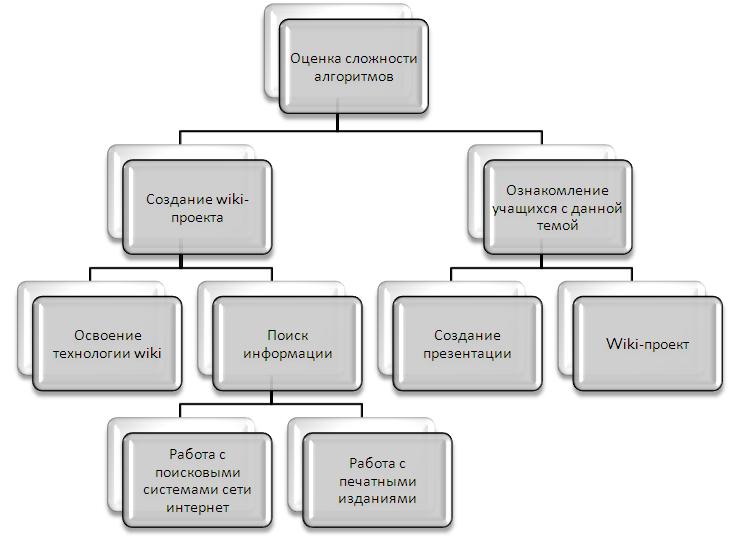
Дерево целей
Презентация
Содержание
- Введение
- Виды сложностей
- Временная сложность
- Пространственная сложность
- Асимптотическая сложность
- Критерии оценки сложности
- Классы сложности
Введение
В информатике, теория сложности вычислений является разделом теории вычислений, изучающим стоимость работы, требуемой для решения вычислительной проблемы. Стоимость обычно измеряется абстрактными понятиями времени и пространства, называемыми вычислительными ресурсами. Время определяется количеством тривиальных шагов, необходимых для решения проблемы, тогда как пространство определяется объёмом памяти или места на носителе данных. Таким образом, в этой области предпринимается попытка ответить на центральный вопрос разработки алгоритмов: «как изменится время исполнения и объём занятой памяти в зависимости от размера входа1) и выхода2)?».
В частности, теория сложности вычислений определяет NP-полные задачи, которые недетерминированная машина Тьюринга может решить за полиномиальное время, тогда как для детерминированной машины Тьюринга полиномиальный алгоритм неизвестен.
Виды сложностей
Временная сложность
Количество элементарных операций, затраченных алгоритмом для решения конкретного экземпляра задачи, зависит не только от размера входных данных, но и от самих данных. Например, количество операций алгоритма сортировки вставками значительно меньше в случае, если входные данные уже отсортированы. Чтобы избежать подобных трудностей, рассматривают понятие временной сложности алгоритма в худшем случае.
Временная сложность алгоритма (в худшем случае) — это функция размера входных и выходных данных, равная максимальному количеству элементарных операций, проделываемых алгоритмом для решения экземпляра задачи указанного размера. Во многих задачах размер выхода не превосходит или пропорционален размеру входа — в этом случае можно рассматривать временную сложность как функцию размера только входных данных.
Пространственная сложность
Пространственная сложность алгоритма (в худшем случае) — это функция размера входных и выходных данных, равная максимальному количеству затраченной памяти, затраченной алгоритмом для решения экземпляра задачи указанного размера. Во многих задачах размер выхода не превосходит или пропорционален размеру входа — в этом случае можно рассматривать пространственную сложность как функцию размера только входных данных.
Асимптотическая сложность
Несмотря на то, что функция временной сложности алгоритма в некоторых случаях может быть определена точно, в большинстве случаев искать точное её значение бессмысленно. Дело в том, что, во-первых, точное значение временной сложности зависит от определения элементарных операций (например, сложность можно измерять в количестве арифметических операций или операций на машине Тьюринга), а во-вторых, при увеличении размера входных данных вклад постоянных множителей и слагаемых низших порядков, фигурирующие в выражении для точного времени работы, становится крайне незначительным.
Асимптотическая сложность - рассмотрение входных данных большого размера и оценка порядка роста времени работы алгоритма. Обычно алгоритм с меньшей асимптотической сложностью является более эффективным для всех входных данных, за исключением лишь, возможно, данных малого размера.
Для записи асимтотической сложности алгоритмов используются следующие обозначения:
Критерии оценки сложности
- Если создаваемая программа будет использована только несколько раз, тогда стоимость написания и отладки программы будет доминировать в общей стоимости программы. В этом случае следует предпочесть алгоритм, наиболее простой для реализации.
- Если программа будет работать только с «малыми» входными данными, то степень роста времени выполнения будет иметь меньшее значение, чем константа, присутствующая в формуле времени выполнения. Вместе с тем и понятие «малости» входных данных зависит от точного времени выполнения конкурирующих алгоритмов. Существуют алгоритмы, такие как алгоритм целочисленного умножения, асимптотически самые эффективные, но которые никогда не используют на практике даже для больших задач, так как их константы пропорциональности значительно превосходят подобные константы других, более простых и менее «эффективных» алгоритмов.
- Эффективные, но сложные алгоритмы могут быть нежелательными, если готовые программы будут поддерживать лица, не участвующие в написании этих программ.
- Известно несколько примеров, когда эффективные алгоритмы требуют таких больших объемов машинной памяти (без возможности использования более медленных внешних средств хранения), что этот фактор сводит на нет преимущество «эффективности» алгоритма.
- В численных алгоритмах точность и устойчивость алгоритмов не менее важны, чем их временная эффективность.
Классы сложности
Класс P вмещает все те проблемы, решение которых считается «быстрым», то есть полиномиально зависящим от размера входа. Сюда относится сортировка, поиск во множестве, выяснение связности графов и многие другие.
Класс NP содержит задачи, которые недетерминированная машина Тьюринга в состоянии решить за полиномиальное количество времени. Следует заметить, что недерминированная машина Тьюринга является лишь абстрактной моделью, в то время как современные компьютеры соответствуют детерминированной машины Тьюринга с ограниченной памятью. Таким образом, класс NP включает в себя класс P, а также некоторые проблемы, для решения которых известны лишь алгоритмы, экспоненциально зависящие от размера входа (т.е. неэффективные для больших входов). В класс NP входят многие знаменитые проблемы, такие как задача коммивояжёра, задача выполнимости булевых формул, факторизация и др.
Примеры
если при увеличении размера входного массива в 2 раза количество итераций алгоритма по его обработке возрастёт в 4 раза, то это - квадратичная зависимость  .
.
Можно эту функцию получить и экспериментально - нужно просто замерить время работы алгоритма на различных объёмах входных данных и построить график.
Может оказаться, что алгоритм с большей трудоёмкостью будет более эффективен на небольших объемах данных, поскольку коэффициенты при её расчёте обычно опускаются и считается предельная оценка при 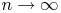 . Например, алгоритм
. Например, алгоритм  будет явно эффективнее на небольших объемах, чем
будет явно эффективнее на небольших объемах, чем 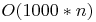 . Поэтому Вам, возможно, будет интереснее замерить реальную производительность и получить графическую зависимость экспериментально.
. Поэтому Вам, возможно, будет интереснее замерить реальную производительность и получить графическую зависимость экспериментально.